Die Subtraktion im BCD Code wird auf die Addition eines Komplements (Ergänzung, Vervollständigung) zurückgeführt. Dabei unterscheidet man zwischen dem Neunerkomplement und dem Zehnerkomplement. Die Subtraktion im BCD-Code wird auf die Addition des Zehnerkomplementes zurückgeführt. Aufpassen muss man bei der Subtraktion, dass man nicht in die Pseudotetraden rutscht. Ist dies der Fall, muss man die Zahl 6 (0110) addieren. Folgende Beispiele sollen die Subtraktion im BCD Code verdeutlichen.

Beispiel 1:
Die Aufgabe lautet: 9 (Minuend) -8 (Subtrahend) = ?. Um auf das Ergebnis zukommen, benutzt man das Zehnerkomplement. Dabei kann man einfach den Subtrahend in diesem Fall von 10 abziehen. 10-8 =2. Also muss zur 9 die 2 addiert werden. Hat man das gemacht, muss man weiter schauen, ob eine Pseudotetrade heraus kommt. Auch dies ist in diesem Beispiel der Fall. Deshalb muss zu diesem Ergebnis noch die Zahl 6 (0110) summiert werden. Anbei die Rechnung:

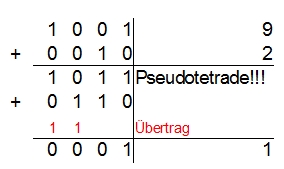
Beispiel 2:
Das zweite Beispiel funktioniert wie das erste. Diesmal lautet die Aufgabe 9 – 6 = ?. Das Zehnerkomplement zu 6 ist 4, deshalb werden 4 zur 9 addiert. Auch hier ist das erste Ergebnis wieder eine Pseudotentrade.

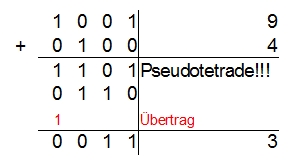
Beispiel 3:
Beim dritten Beispiel, Aufgabe: 9 – 2 = ?, hat man nun zwar keine Pseudotetrade, dennoch muss man mit 6 (0110) ergänzen, da es einen Übertrag gibt. Und auch hier gelangt man so auf das richtige Ergebnis: 7.

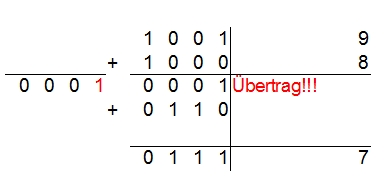
Beispiel 4:
Wagen wir uns an etwas größere Zahlen. Die Aufgabe lautet: 53 – 16 = ? Das Prinzip ist auch hier das selbe, wie bei den vorangegangenen Beispielen. Diesmal muss man den Subtrahend von 100 abziehen. 100-16=84. Also muss die 84 zur 53 aufsummiert werden.

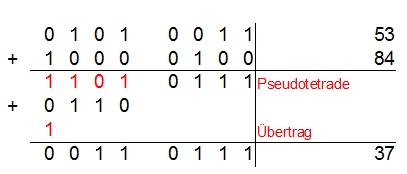
Negative BCD Zahlen
Zum Schluss kommen wir noch zu negative BCD Zahlen. Solche negative Zahlen erkennt man im übrigen, wenn es bei der Addition des Zehnerkomplements mit der BCD-Tetrade kein Übertrag in eine 5. Stelle gibt.

Anbei die Aufgabe 5 – 8 = ?

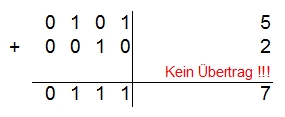
Erstmal der Hinweis, dass es keinen Übertrag gibt, damit muss es sich beim Ergebnis um eine negative Zahl handeln. Allerdings ist 5-8 nicht 7. Damit man den Betrag der negativen Zahl ablesen kann, muss man auf eine Rückkomplementierung zurückgreifen. Der Betrag der negativen Zahl ist ihr Zehnerkomplement. Klingt wieder komplizierter als es ist. In unserem Fall müssen wir lediglich vom Ergebnis 10 abziehen. Also: 7 – 10 = -3. Voila, schon haben wir das Ergebnis von unserer eigentlichen Aufgabe 5-8.